Pricing of a Defaultable Bond with a Reduced-Form Model (Part I & II)

In this post, we will see how to price a risky bond with a reduced-form model for default risk.

We assume in this first part that there is no recovery rate in case of default.

I. Pricing of a Risky Zero-Coupon Bond with Zero Recovery Rate in Case of Default

Pricing of a Risk-Free Zero-Coupon Bond

First, we consider a risk-free zero-coupon bond.

The buyer of the bond will receive the face value of the bond (100) at the maturity of the bond and he will pay at t = 0 a price (PriceZC_RF) equal to the face value time the discount factor. There is no payment of coupons here.

The discout factor is equal to exp(-r.T) with continuous compounding.

Pricing of a Risky Zero-Coupon Bond

Now we consider a risky zero coupon bond. We assume zero recovery rate. There is the payment of principal at maturity T if there is no default before, the price of the bond is P. In case of default before the maturity of the bond, the bondholder will not recover any part of his initial investment.

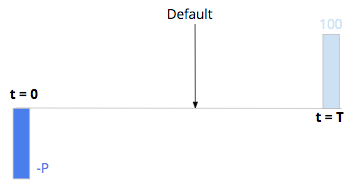
We model the default risk with a constant default intensity model (link). The probability that there is no default before T P(τ≥T), the survival probability, is:

λ is the default intensity of the issuer of the bond, τ the times of default.

If there is a default before T, the bondholder will not recover any part of the principal of the bond. The probability that there is a default before T is 1- exp(-λ.T).

With no arbitrage assumption the price of the bond at t = 0 (PriceZC_R) is the discounted expectation of the final payoff:

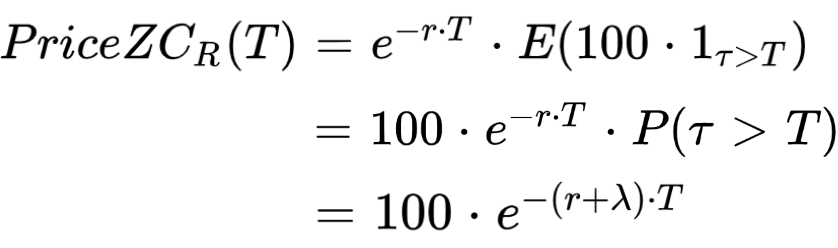
The price of the risky zero coupon bond is equal to the price of the risk free zero coupon bond times the survival probability.

The zero coupon bond has a lower price compared to the risk free bond. If an investor buy the bond, keep it until its expiry and the issuer does not default, he could expect a higher return, a positive carry to compensate for the default risk of the bond.

Estimation of the default intensity from market prices

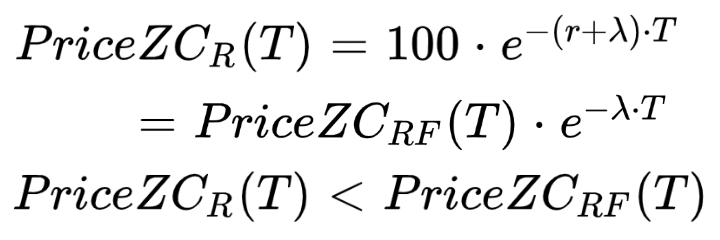
The survival probability can be estimated as the ratio between the prices of the risk free and the risky zero coupon bond.

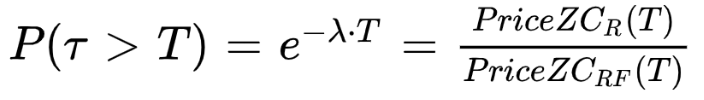
And we get an estimation of the default intensity from market prices.

Relationship between default intensity and z-spread

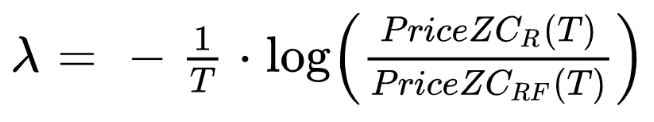
The z-spread is the spread that needs to be added to the risk-free rate to obtain the price of the risky bond. It is the additional compensation asked by investors for taking that risk.

With Z the z-spread of the risky zero coupon bond we have:

With continous compounding we get:

r + z is the bond yield.

We see that in this framework the z-spread is equal to the default intensity of the bond.

This is only true if we assume zero recovery rate.

II. Pricing of a Risky Bond with Zero Recovery Rate

Pricing of a Risk-Free Bond

First, we consider a risk-free bond paying a coupon C, with principal 100 and maturity T.

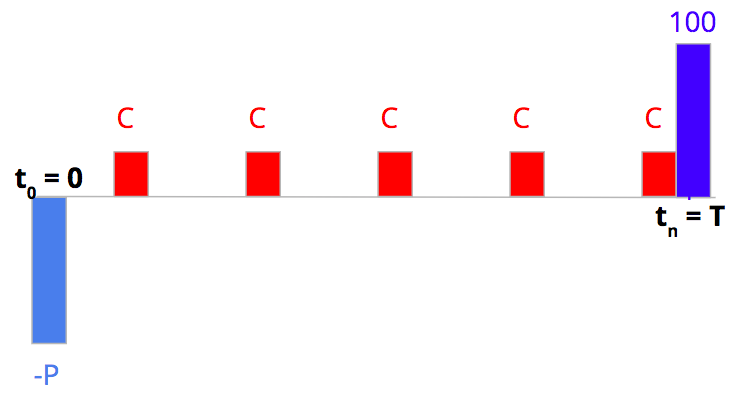
with R_ti the risk free rate, its price P_RF is, by non arbitrage:

Assuming continuous compounding and constant interest rate r the price of the risk-free bond is:

Pricing of a Risky Bond

Now we consider a risky bond paying coupons. Coupons are paid as long as there is no default. We assume zero recovery rate. In case of default, the bondholder will not recover any part of his initial investment.

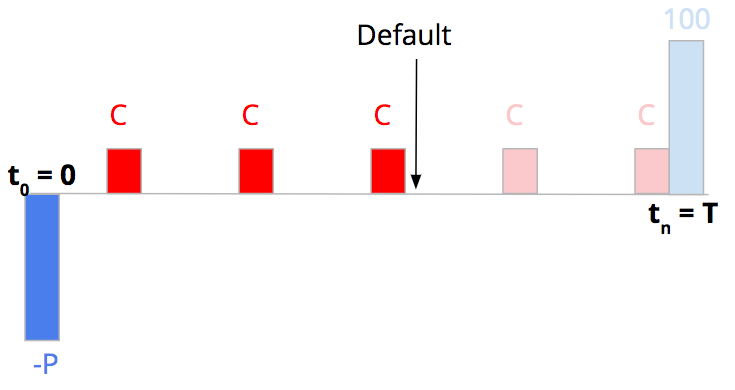
The sum of the discounted cash-flow is:

with continuous compounding:

The price of the risky bond is the expectation of the sum of the discounted cash-flows:

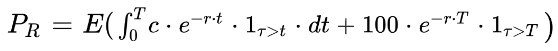
The expectation of the indicator function at t is the survival probability, the probability that there is no default before t:

With a constant default intensity model we obtain:

And if we calculate the integral term we obtain this expression:

It can be rewritten like this:

We see that the price of the risky bond is higher than 100 if the coupon of the bond divided by 100 is strictly higher than the sum of the risk free interest rate r and the default intensity lambda.

If will be below 100 if it is strictly below.

And the bond will be at par if the two are equal.

Risky Duration

The last term is the risky duration. It is the integral of the discount factor times the survival probability between 0 and T.

The risky duration is lower than the non risky duration as it includes as well the risk of default before the expiry of the bond. The higher the default risk of the issuer, the lower the risky duration.

When lambda tends to infinity, meaning that the default probability tends to 1, the risky duration tends to zero, and the bond price as well.

Below is the Python code with the calculation of the riskyduration and the bond price assuming zero recovery rate in case of default.

Python Code

import matplotlib.pyplot as plt
plt.style.use('ggplot')
import numpy as np

lambda_ = np.arange(0,10,0.01)
r = 0.03 #risk-free interest rate
T = 5 #time to maturity of the bond in years
riskyduration = (1 - np.exp(-(r + lambda_) * T)) / (r + lambda_)

plt.figure(figsize=(10, 6))
plt.plot(lambda_, riskyduration)
plt.title('Risky Duration as a Function of Default Intensity')
plt.xlabel('Default Intensity')
plt.ylabel('Risky Duration')
plt.show()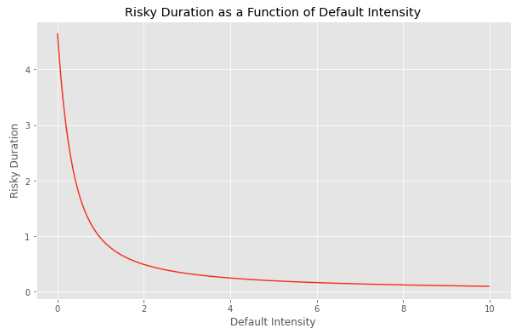

c = 6 #coupon
price = 100 * (1 + (c / 100 - r - lambda_) * riskyduration)

plt.figure(figsize=(10, 6))
plt.plot(lambda_, price)
plt.title('Bond Price as a Function of Default Intensity')
plt.xlabel('Default Intensity')
plt.ylabel('Bond Price')
plt.show()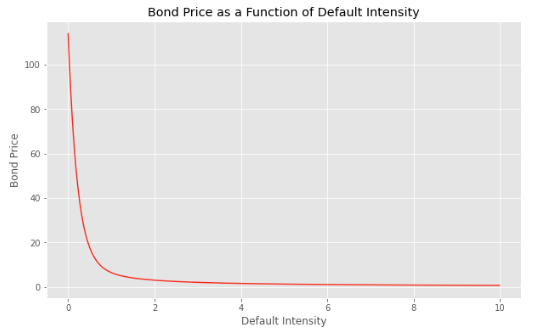

Z-Spread

As a reminder, the z-spread Z is the spread that needs to be added to the risk-free rate to obtain the price of the risky bond. It is the additional compensation asked by investors for taking that risk.

With continuous compounding, we obtain this relationship between the bond price and the z-spread z.

And if we compare it with the expression of the bond price as a function of the default intensity lambda assuming that there is no recovery rate in case of default, we see that the z-spread z is equal to the default intensity lambda.

We will see that this is no more true if the recovery rate is not null in the next part.

This is only true if we assume zero recovery rate.

Watch the Videos

Credit Risk Modelling: Pricing of a Defautable Bond with Reduced-Form Model Part I

Credit Risk Modelling: Pricing of a Defautable Bond with Reduced-Form Model Part II

More about Credit Risk:

Credit Risk: an Introduction

Credit Risk Modelling: the Probability of Default

Credit Risk Modelling: the Default Time Distribution

An Introduction to Reduced-Form Credit Risk Models

Save 10% on All Quant Next Courses with the Coupon Code: QuantNextBlog10

For students and graduates: We offer a 50% discount on all courses, please contact us if you are interested: contact@quant-next.com