The Merton Jump Diffusion Model for Option Pricing

The Merton Jump Diffusion (MJD) model was introduced in a previous article (link). It is an extension of the Black-Scholes model adding a jump part in addition to the diffusion part to model the diffusion of asset prices. We showed how to simulate the asset price, and we analysed the probability density function of the log returns under the MJD model. Particularly we analysed how jump parameters impact the moments of the distribution which is no more gaussian.

In this article we will see how to price vanilla options with the MJD model and how the different parameters impact the implied volatility smile.

The Python code is available at the end of the article.

Merton Jump Diffusion (MJD) Model

Merton in 1976 proposed the following stochastic differential equation (SDE) for the asset price S_t:

It contains:

• A diffusion part with a standard wiener process W(t) (link):

μ: annualised expected return on the asset price, σ: annualised volatility of the asset price, W_t: Brownian motion.

• A jump part with a compound Poisson process Q(t):

Q_t: compound Poisson process

Y_i: price ratio associated with the i-th jump happening at the random time t_i. (Y_i) are i.i.d, following a lognormal distribution, and are independent of W_t and N_t, N_t being a Poisson process (link) with intensity λ. E(Q_t) = λ.k.t, so Q_t – λ.k.t is a martingale.

There is an explicit solution of this SDE:

Option Pricing with Merton Jump Diffusion Model

In its reference paper, Merton assumed that jumps are pure non systemic risks and are uncorrelated with market.

In this framework the risk-neutral probability used to price option will not change the jump measure. It will only impact the continuous part.

Under the risk-neutral probability (which does not change the jump measure) the discounted expectation of the asset price is a martingale if and only if μ = r (proof in Addendum 1).

So under the risk neutral probability, the asset price S_t follows the SDE:

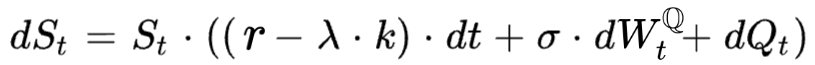
The logarithm of the asset price knowing the number of jumps follows a normal distribution:

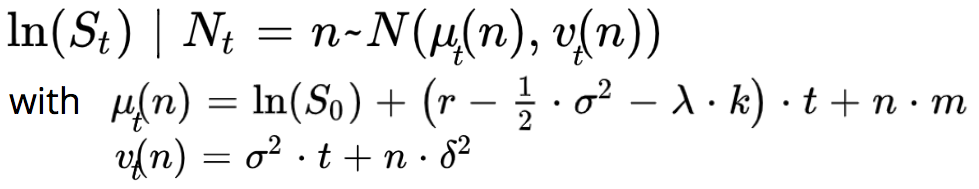
The price of a call option expiring at T with strike price K is the discounted expectation of the final payoff under the risk neutral probability.

In the MJD model, it can be expressed as following:

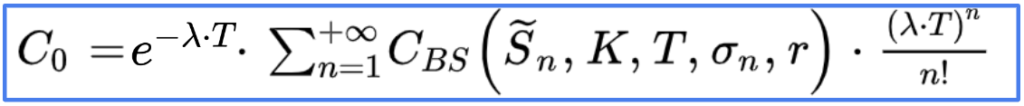
With

C_BS the Black-Scholes price of a call option,

Proof in addendum 2.

Volatility Smile with the MJD Model

Jumps add volatility and smile

Option prices and so Black-Scholes implied volatilities are always higher with the MJD model compared to the Black-Scholes model when using a similar volatility parameter σ as jumps create an additional source of randomness.

Moreover, as illustrated on the chart below, the implied volatility curve is no more flat in the MJD model, jumps create a smile.

In order to draw the Black-Scholes volatility smile implied by a set of parameters of the MJD model, we fix the parameters, we calculate for a range of strike prices the call option price, and then we deduce the Black-Scholes implied volatility with numerical method (link).

Volatility Smile with the MJD Model

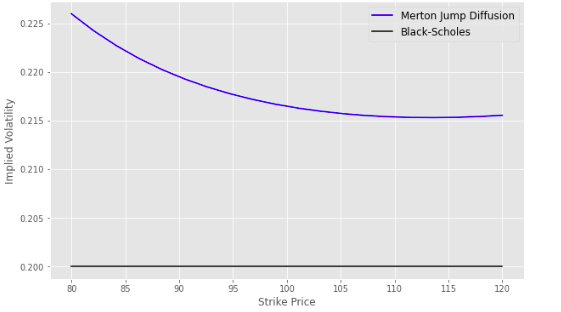
Parameters: asset price S0 = 100, time to maturity T = 1yrs, risk-free interest rate r = 5%, volatility sigma = 20%, jump intensity lambda = 10%, average jump size m = -0.1, jump volatility delta = 0.3.

This is in line with the implied return distribution when using the MJD model. We showed in a previous article (link), that in addition to an increase of the standard deviation of the log-returns, jumps adds tail-risk (kurtosis) and asymmetry (skewness), positive or negative depending on the sign of the average jump.

Impact of the asset volatility level

As expected, the asset volatility level sigma impact the level of the implied volatility curve.

Impact of asset volatility level on the volatility smile with the MJD model

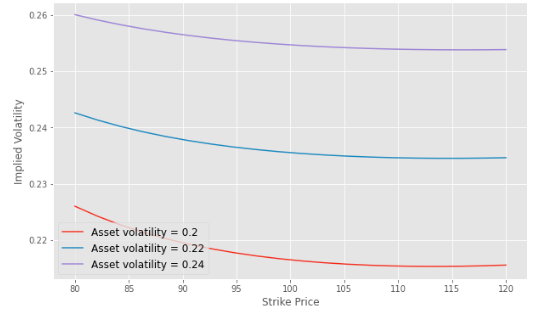
Parameters: asset price S0 = 100, time to maturity T = 1yrs, risk-free interest rate r = 5%, volatility sigma = 20%, 22%, 24%, jump intensity lambda = 10%, average jump size m = -0.1, jump volatility delta = 0.3.

Impact of the jump size

The sign of the average jump size impacts the sign of the skewness of the volatility smile. A positive (resp. negative) average jump size would lead to more tail risk on the upside (resp. downside), leading to higher implied volatilites on the right-hand side (resp. left side), i.e. a positive (resp. negative) skewness.

The size of the jumps in absolute value will impact the level of the skewness negative, or positive, depending on the sign of the average jump.

Impact of the jump size on the volatility smile with the MJD model

Parameters: asset price S0 = 100, time to maturity T = 1yrs, risk-free interest rate r = 5%, volatility sigma = 20%, jump intensity lambda = 10%, average jump size m = -0.1, 0, 0.1, jump volatility delta = 0.3.

Impact of the jump volatility

A higher volatility of jumps will increase the volatility of the asset, as it will increase the probability to have important movements of the asset price on the downside and on the upside before the expiry of the option. It will increase as well the smile of volatility with more tail risk on both sides.

Impact of the jump volatility on the volatility smile with the MJD model

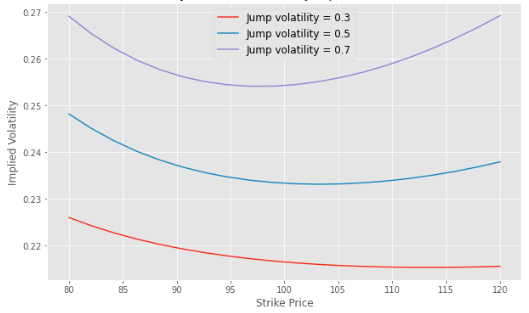
Parameters: asset price S0 = 100, time to maturity T = 1yrs, risk-free interest rate r = 5%, volatility sigma = 20%, jump intensity lambda = 10%, average jump size m = -0.1, jump volatility delta = 0.3, 0.5, 0.7.

Limits of the MJD model

The MJD allows to incorporate jumps in the asset price diffusion, which allows for a more realistic representation of market behaviour, and can be an interesting feature particularly for the pricing of very short term options.

It gives as well more flexibility with three additional parameters compared to the Black-Scholes model to control the frequency of jumps, the average of the standard deviation of jumps.

However, more flexibility comes in general with more complexity.

Several parameters can have similar effects on the volatility smile leading to potential difficulties to estimate parameters in an accurate and stable manner.

Moreover, contrary to the Heston model for example (link), the Merton model is unable to control the term structure of the volatility smile, with limited possible shapes of the volatility surfaces.

References

Merton, R. C. (1976) “Option Pricing When underlying stock returns are discontinuous”, Journal of Financial Economics, 3, 125-144

K. Matsuda (2004) “Introduction to merton jump diffusion model”, Department of Economics. The Graduate Center, The City University of New York.

Save 10% on All Quant Next Courses with the Coupon Code: QuantNextBlog10

For students and graduates: We offer a 50% discount on all courses, please contact us if you are interested: contact@quant-next.com

Python code

Import libraries

import numpy as np
from scipy.stats import norm
import math

Call price with Black-Scholes model

def CallPriceBS(S, sigma, K, T, r):
    d1 = (math.log(S / K) + (r + .5 * sigma**2) * T) / (sigma * T**.5)
    d2 = d1 - sigma * T**0.5
    n1 = norm.cdf(d1)
    n2 = norm.cdf(d2)
    DF = math.exp(-r * T)
    price=S * n1 - K * DF * n2
    return price

Call price with Merton Jump Diffusion model

def CallPriceMJD(S, sigma, K, T, r, lambda_, m, delta, N=50):

    price = 0.0
    k_ = np.exp(m + .5 * delta**2) - 1
    for n in range(N):
        # Adjusted parameters for n jumps
        sigma_n = np.sqrt(sigma ** 2 + (n / T) * delta ** 2)
        S_n = S * np.exp(-lambda_ * k_ * T + (m + .5 * delta**2) * n)
        
        # Poisson probability of n jumps
        poisson_proba = np.exp(-lambda_ * T) * (lambda_ * T) ** n / np.math.factorial(n)
        
        # Black-Scholes price with jump-adjusted parameters
        priceBS = CallPriceBS(S_n, sigma_n, K, T, r)
        
        # Summing up the weighted price by Poisson probability
        price += poisson_proba * priceBS
        
    return price

# Parameters
S = 100      # Underlying stock price
K = 100      # Strike price
T = 1.0      # Time to maturity (in years)
r = .05     # Risk-free rate
sigma = .2  # Volatility
lambda_ = .1   # Jump intensity (average jumps per year)
m = -.1  # Average jump size
delta = .3  # Jump volatility

call_price = CallPriceMJD(S, sigma, K, T, r, lambda_, m, delta)
print("Call Price (Merton Jump Diffusion):", call_price)

Addendum

Addendum 1

Let’s demonstrate that with μ = r we have:

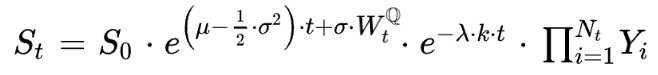
Addendum 2

Using the conditional expectation of the price of the final payoff we have:

With:

the probability to have n jumps.

ln(S_T)|N_T=n follows a normal distribution and S_T|N_T=n can be written as:

It can be rewritten as:

With

We obtain for the asset price at T an expression similar to the one in the Black-Scholes framework with an initial price equal to:

and a volatility parameter equal to