Quant and Trading Interview Questions about Option Greeks and Risk Management

It is crucial for quant or trading positions to have a strong understanding of the main option Greeks and how they can be used for risk management purposes.

You will find below several questions you could be asked in an interview for a quant or a trading role, with possible answers.

Save 10% on All Quant Next Courses with the Coupon Code: QuantNextBlog10

For students and graduates: We offer a 50% discount on all courses, please contact us if you are interested: contact@quant-next.com

1. What are the main option Greeks and what are they used for?

Option Greeks are used to assess and manage the risk associated with options positions. They are key for pricing options, managing risk, and building options strategies effectively in quantitative finance and trading.

The Black-Scholes price of an option P(t, S, σ, r) is a function of time (t), the stock price (S), the implied volatility (σ) and interest rate (r). Theta (θ), Delta (Δ), Vega (ν), Rho (ρ) are the first order Greeks:

• The Theta (θ) or time decay measures the rate at which the value of the option declines due to the passage of time.
• The Delta (Δ) of an option measures the change in the option’s price resulting from a change in the underlying asset. For option traders, minus delta indicates how many underlying assets are needed to be purchased or sold to hedge the directional exposure of the option position. For call options, delta ranges from 0 to 1, while for put options, it ranges from -1 to 0.
• Vega (ν) measures the change in the option’s price resulting from a change in the implied volatility. Vega is essential because it helps traders assess how sensitive their options positions are to shifts in market volatility.
• Rho (ρ) measures the option’s sensitivity to changes in the risk-free rate of interest. It is most relevant for long-term options and is less critical for short-term ones.

The most important second order Greeks are:

• Gamma (Γ): it measures the rate of change of the delta of an option relative to the underlying asset price. It is the second order partial derivative of the value of the option with respect to the price of the underlying asset.
• Vanna: it measures the option’s sensitivity to small changes in the underlying asset price and volatility.  It is the sensitivity of the delta to changes in the volatility or the sensitivity of the vega to changes in the underlying asset price.
• Volga or Vomma: it measures the sensitivity of the vega to a change in the implied volatility.  It is the second order partial derivative of the price of the option with respect to the implied volatility.
• Charm: it is the option’s sensitivity to small changes in the underlying asset price and passage of time. It is also the sensitivity of the delta to the passage of time or the sensitivity of the theta to changes in the underlying asset price.

2. Can you please write the P&L decomposition of an option portfolio with these Greeks?

With a second order Taylor expansion of the option value over a short time interval delta t we can decompose the variation of the option price as following.

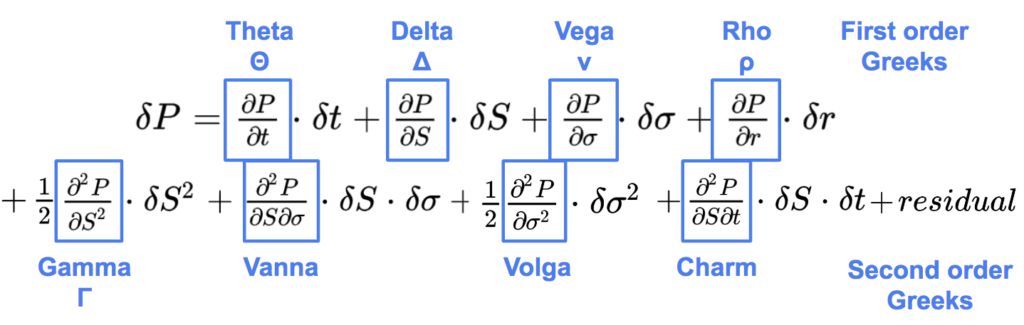
The residual regroups other second order and higher order sensitivities.

3. How do the Delta, Theta, Vega and Gamma change for call options versus put options?

For call options, the Delta is positive. The price of the option increases with the underlying asset price as it becomes more likely to be executed. For put options it is the opposite, the Delta is negative, the price of the put option decreases when the underlying asset price increases as it becomes more out-of-the-money with a lower probability to be exercised.

Theta, Vega, and Gamma behave similarly for both call and put options but may differ in magnitude depending on the specific option contract.

Theta is typically negative for both call and put options. As time passes and the option gets closer to expiry, its premium decreases, the value of the option erodes due to time decay.

Vega is positive for both call and put options. It measures the sensitivity of the option price to changes in implied volatility. As the implied volatility increases, the price of both calls and puts tends to increase.

Gamma, which measures the rate of change of the delta with respect to the underlying asset price is positive for both call and put options. It is a measure of the convexity of the option, it is larger for at-the-money options and it decreases as options are more out-of-the-money.

Below is a series of questions related to the Black-Scholes delta:

4. What is approximately the delta of an at-the-money call option when it is close to expire? Why? Avoid the maths as much as possible in your explanations.

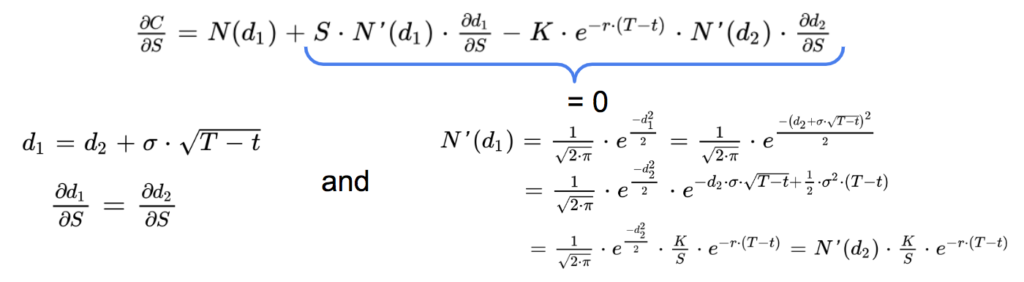
The call option gives the right to buy the underlying asset at a given price K. If the asset price is very close to K, the option is at-the-money (ATM), then it has approximately:

• 50% chance of being exercised. If it is the case, then the delta would be 1.
• 50% chance of not being exercised, then the delta would be equal to 0.

So the delta of an ATM call option close to expire is close to 0.5.

5. Is the delta of a call option higher or lower than the probability of being exercised? Why?

The delta of a call option is higher than the probability that the option will be exercised.

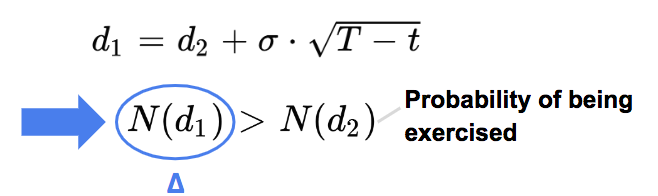
In addition to the probability of being exercised, the delta incorporates by how far the option can be in-the-money.

6. Write the Black-Scholes formula for a call option and identify the Delta in the Formula. What is the second term? We assume that there is no dividend payment in this question and the following ones.

7. Do the same for a European Put Option.

8. Verify that we have the call / put parity. What is the relationship between the delta of a call and a put option on the same underlying asset with same expiry and strike?

9. Demonstrate that the delta of a call option is equal to N(d1) by calculating the partial derivatives of the Black-Scholes call price with respect to the underlying asset price.

10. Draw the delta profiles of a call option far from expiry and close to expiry as a function of the underlying asset price.

11. Do the same for a digital call option.

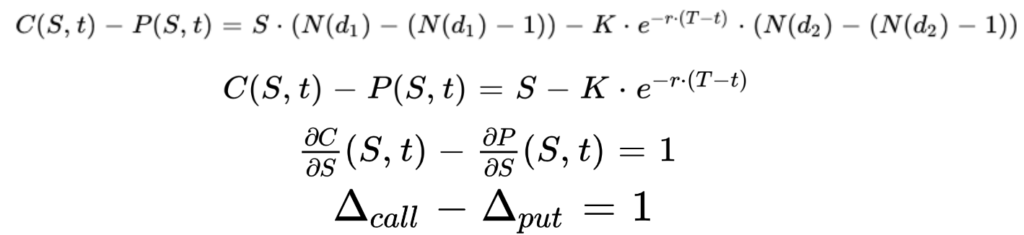
For a digital call option, the delta will tend to zero on the right and on the left of the strike price, while it will tend to infinity at the strike price when the time to expiry tends to zero.

12. Discuss the concept of dynamic Delta-hedging vs static Delta-hedging. When and why would a trader choose one approach over the other?

Dynamic Delta-hedging involves continuously adjusting the hedge ratio based on changing market conditions, while static Delta-hedging maintains a constant hedge ratio.

Traders may choose dynamic Delta hedging when they anticipate frequent and significant changes in market conditions, while static Delta hedging can be simpler for more stable markets.

Dynamic delta hedging comes with higher transaction costs, so the trader has to be careful in the frequency of his rebalancing.

Below is a series of questions related to the gamma of an option:

13. What is the gamma of an option?

The gamma (Γ) measures the rate of change of the delta (Δ) of an option:

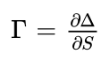
It determines how stable how stable the delta is.  A higher gamma means a more important change of the delta when the underlying asset price changes.

It is the second order partial derivative of the value of the option (P) with respect to the price of the underlying asset (S):

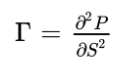
It measures the convexity of the price of the option with respect to the underlying asset price.

14. Draw the P&L profile of a call option as a function of the asset price and its delta

15. Identify the P&L of a delta-hedged position on the previous chart

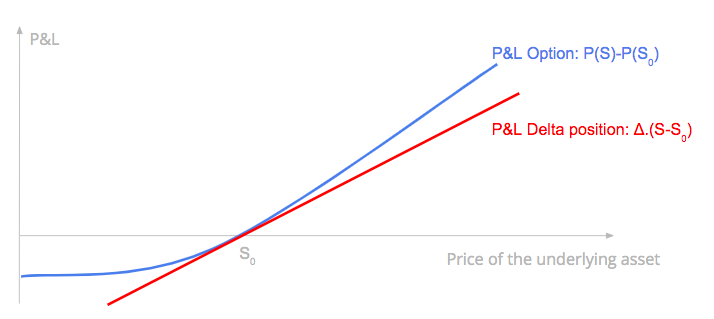
The P&L of a delta-hedged position is the difference between the P&L of the option, and the P&L of the delta position.

16. How can you approximate the P&L of a delta-hedged position with the Gamma of the option?

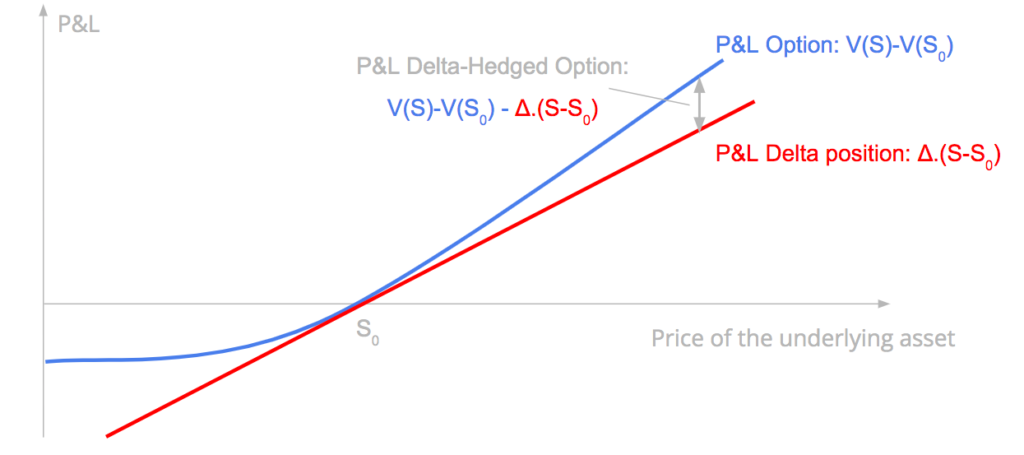
The P&L of a long delta-hedged option position has a quadratic relationship with the change of the underlying asset price at the first order and is a function of the gamma. It means that the strategy is likely to gain if there is a sudden important movement of the underlying asset on the upside or on the downside, and the gain will be at the first order proportional to the gamma of the option.

17. Write the decomposition of the P&L of a long delta-hedged option position between t and t+ẟt from its Gamma and its Theta P&Ls. If the implied volatility is higher than the realised volatility, is the P&L of the position positive or negative? We assume that the risk-free interest rate is equal to zero, there is no dividend payment, and there is no change of the implied volatility.

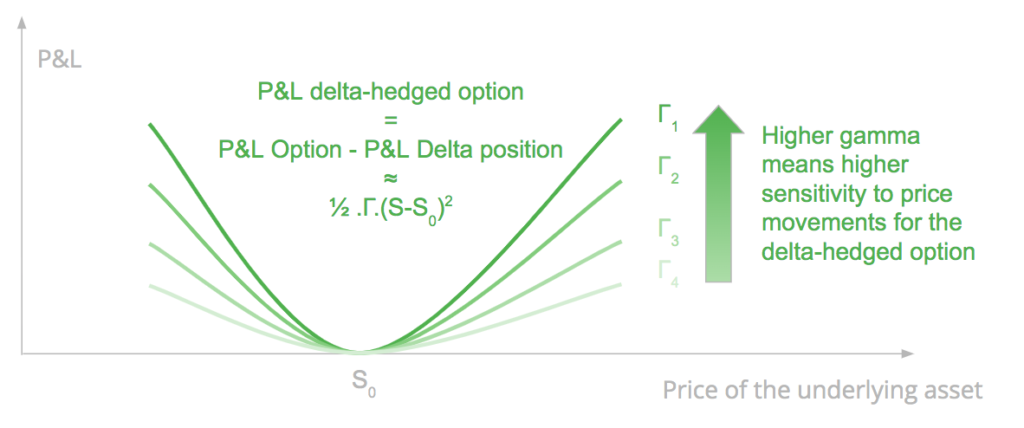
Theta, the time decay of the option, is the cost of gamma. It is the cost for the convexity of the option measured by the gamma.

We have, with σ_r the realised volatility:

And if we assume that r = q = 0 we have:

So the P&L of the delta-hedged option between t and t + δt is close to:

when neglecting higher order Greeks.

If the implied volatility is higher than the realised volatility, the P&L of the strategy is negative.

18. Let’s assume stock price = 100, option gamma = 0.2, option delta = 0.5,  and that the stock price goes up + 5% very quickly. What is approximately the P&L of a long position on the option (quantity = 1). Tips: decompose the P&L with delta and gamma neglecting other Greeks.

The P&L of the long position on the option can be approximated as following, keeping the Delta and Gamma P&L and neglecting other Greeks:

Delta P&L = 0.5 x 5% x 100 = 2.5

Gamma P&L = 1/2 x 0.2 x (5% x 100) ^2 = 2.5

P&L ≈ Delta P&L + Gamma P&L

P&L ≈ 2.5 + 2.5 = 5

19. How does the gamma varies as a function of the stock price?

The gamma is maximum when the option is close to the money, when the stock price is close to the strike price, as the option is more convex around the strike price.

20. How does the gamma of an at-the-money (ATM) option varies when the option gets closer to expiry?

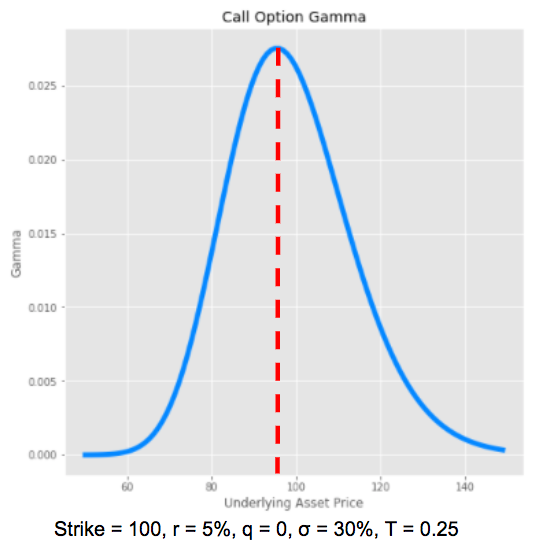
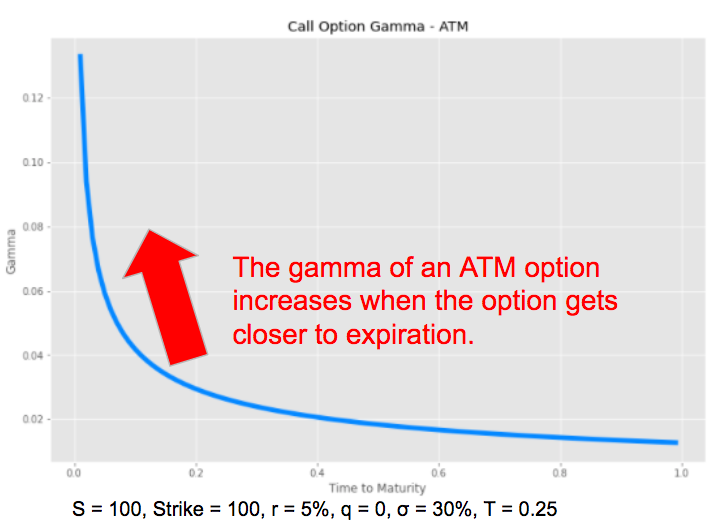
The gamma of an ATM option increases when the option gets closer to expiration.  The gamma measures the instability of the delta, which is maximum when the option is at the money and approaches expiry.

21. How does the gamma of an out-of-the-money (OTM) option varies when the option gets closer to expiry?

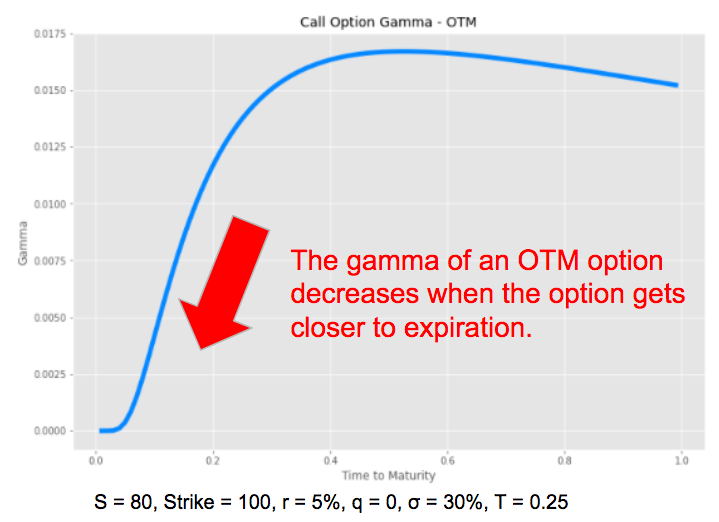
It is the opposite when the option is OTM, the gamma decreases and tends to zero when the option gets closer to expiry.

22. Which instruments you need to hedge the gamma risk of an option portfolio?

Via a delta-hedging of the option portfolio, with the underlying asset directly or futures / forwards, we are able to cancel the directional risk, the delta of the portfolio but not the gamma risk. In order to offset the gamma exposure, we need to use another option on the same underlying asset.

23. Let’s consider an option portfolio on a certain asset, which has a delta equals to 0.5 while its gamma is close to 0.02. We consider another option on the same underlying asset, its delta is 0.2 while its gamma is 0.01. How can you hedge both the delta and the gamma of the option portfolio?

First, we determine the quantity of option to offset the gamma. We need to sell 2 options to cancel the gamma (0.01 x 2 = 0.02). The delta of the new option portfolio is 0.5 – 2 x 0.2 = 0.1. So we need to sell this quantity of asset to offset the delta of the new option portfolio.

Below is a series of questions related to a risk-reversal strategy:

24. What is a risk-reversal strategy?

A risk reversal strategy involves simultaneously buying a call option and selling a put option (long risk-reversal), or vice versa (short risk-reversal), typically with the same expiration date but different strike prices. This strategy is used to speculate on the direction of the underlying asset’s price movement or to hedge exposure to that asset.

25. Can you draw the payoff of such strategy?

26. In order to delta-hedge a long risk-reversal position, will you have to buy or to sell the underlying asset?

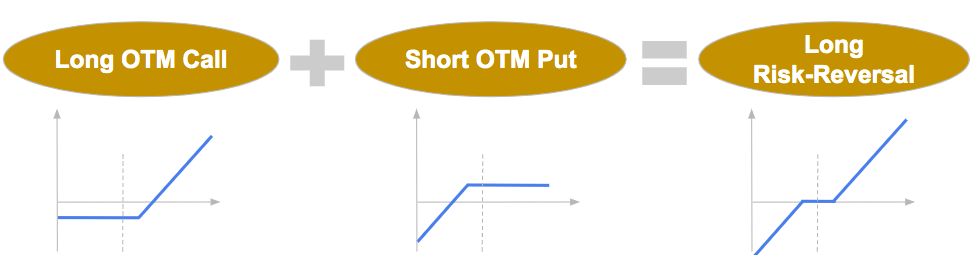
The delta of a long risk-reversal strategy is positive. It is the sum of the delta of a long call position, positive, and a short put position, positive as well.

So we will have to sell the underlying asset in order to offset the delta of the risk-reversal position.

27. What about the gamma of a long risk-reversal?

It depends. The gamma of the long call position is positive while the gamma of the short put is negative. So if we structure the strategy such that the two gamma balance each other, the overall gamma will be near zero.

28. Let’s assume that the gamma of a long risk-reversal strategy was initially close to zero, that both the long call and the short put are out-of-the-money, and that the underlying asset price increases and gets closer to the strike price of the call. How does the gamma of the position evolve?

The gamma of the long call will increase as the option will get closer to the money while the gamma of the short put will be less negative, the option being more out-of-the-money. So all-in-all the gamma of the risk-reversal strategy will increase.

29. Draw the Gamma of a long risk-reversal strategy as a function of the underlying asset price

The initial gamma of the strategy is close to zero.

When the asset price increases (resp. decreases) and gets closer to the strike of the long call (resp. the short put), the gamma increases (resp. decreases).

The value of the gamma is maximal (resp. minimal) when the asset price is close to the strike price of the call option (resp. the put option).

When the asset price is higher (resp. lower) than the strike price of the call option (resp. put option), the gamma starts to decrease (resp. increase) and converges to zero on both sides.

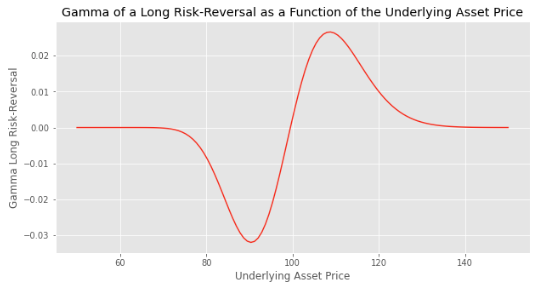
We used the following parameters to plot the chart:

30. And what about the vega of the strategy?

This is very similar to what we did before for the gamma.

The vega of the long call position is positive while the vega of the short put is negative. So if we structure the strategy such that the two vega balance each other, the overall vega will be near zero initially.

When the asset price increases (resp. decreases) and gets closer to the strike of the long call (resp. the short put), the vega increases (resp. decreases).

The value of the vega is maximal (resp. minimal) when the asset price is close to the strike price of the call option (resp. the put option).

When the asset price is higher (resp. lower) than the strike price of the call option (resp. put option), the vega starts to decrease (resp. increase) and converges to zero on both sides.

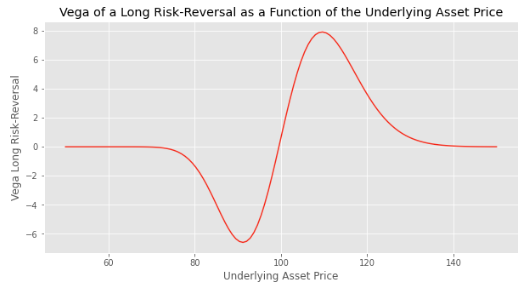
We used the following parameters to plot the chart:

31. What is the vanna of an option?

The vanna measures the option’s sensitivity to small changes in the underlying asset price and volatility.  It is the sensitivity of the delta to changes in the volatility or the sensitivity of the vega to changes in the underlying asset price.

32. Is the vanna of an out-of-the-money call option positive or negative? What about an out-of-the-money put?

While both long call and put options have a positive vega, a higher volatility means a higher price, the Vanna is positive in general for OTM call option and negative for OTM put option.

When the option is very OTM its delta decreases in absolute value and tends to zero particularly when the option becomes close to expiry. As the implied volatility increases, the probability that the option moves in the money and that the delta becomes more positive for call options and more negative for put options increases.

So a higher volatility means a higher delta for an OTM call and a lower delta for an OTM put.

33. So what about the vanna of our long risk-reversal strategy?

A long risk-reversal strategy is the sum of a long call and a short put positions. The vanna of each leg is positive initially, when both options are out-of-the-money, so the vanna of the risk-reversal strategy is positive.

We can see it on the previous chart which shows the vega of the risk-reversal as a function of the asset price. The vanna is the slope of the curve. So we see that it is positive initially, while it will become negative if the call or the put option are in the money.

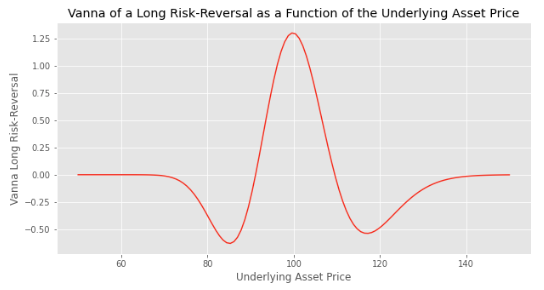
We used the following parameters to plot the chart:

Below is a series of questions related to straddle, strangle and butterfly strategies:

34. What are the main risks of a long straddle strategy?

A long straddle is an option strategy where an investor simultaneously purchases both a call option and a put option with the same strike price and expiration date. The main goal of a long straddle is to benefit from significant price movement in the underlying asset, regardless of whether it moves up or down.

If the underlying asset price is close to the strike price at the maturity of the option, the strategy is likely to finish with a loss, close to the premium of the options.

35. Can you draw the P&L profile of a long stradddle strategy at the maturity of the option?

36. Can you characterise a long straddle in terms of Greeks?

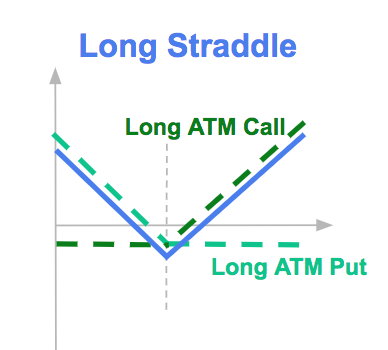
In terms of Greeks, a long straddle has:

• A low delta, has the positive delta of the long call option is offset by the negative delta of the long put option.
• A negative Theta (time decay), both the call and the put options lose value as time passes.
• A positive Gamma as both the long call and the long put have a positive gamma exposure. It means that the strategy would gain if there is an important movement of the underlying asset on both sides, with a gamma P&L higher than the negative time decay.
• A positive Vega, as both the long call and the long put positions have a positive Vega exposure. It means that the strategy would benefit if there is an increase of the implied volatility while it woud lead to losses if the implied volatility decreases.

37. How the delta of the straddle option would evolve if the underlying asset increases? So how would you hedge this directional risk?

The delta of the straddle option initially close to zero would become positive, as the delta (positive) of the long call option, in-the-money (ITM), would be higher in absolute value than the delta (negative) of the put option, out-of-the-money (OTM). You will need to sell the underlying asset in order to hedge it.

37. What is a long strangle strategy? What are its Greeks?

A long strangle is a strategy where the investor purchases out-of-the-money (OTM) call and put options on the same underlying asset with the same expiry date. The investor is likely to gain if there is an important movement of the underlying asset on the upside or on the downside. The cost of the strangle option is lower than the cost of the straddle option on the same underlying with the same maturity as it is buying more OTM options.

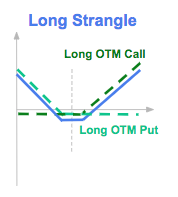
Its Greeks are similar to the long straddle option: low Delta, negative Theta, positive Gamma and positive Vega.

38. What is the final payoff of a strategy which is long a straddle and short a strangle option strategy on the same underlying asset with the same expiry date?

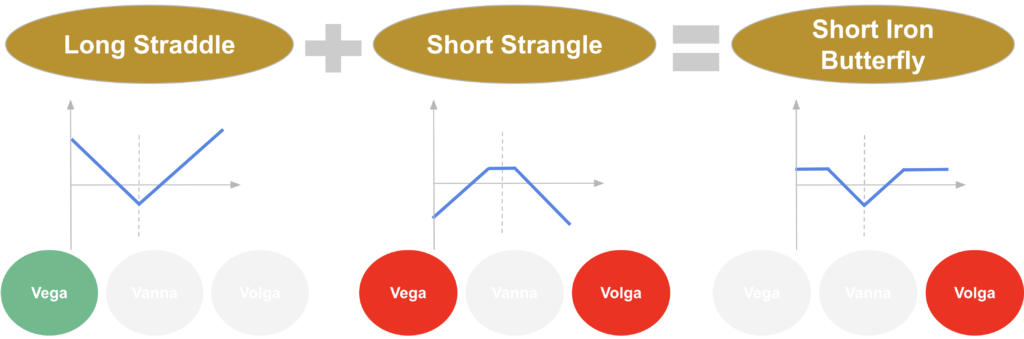
The strategy is buying ATM call and put options and selling OTM put and call options. We draw in blue below the final payoff of the strategy.

39. What is the name of such strategy? Does it have a positive or a negative premium? When is it likely to gain?

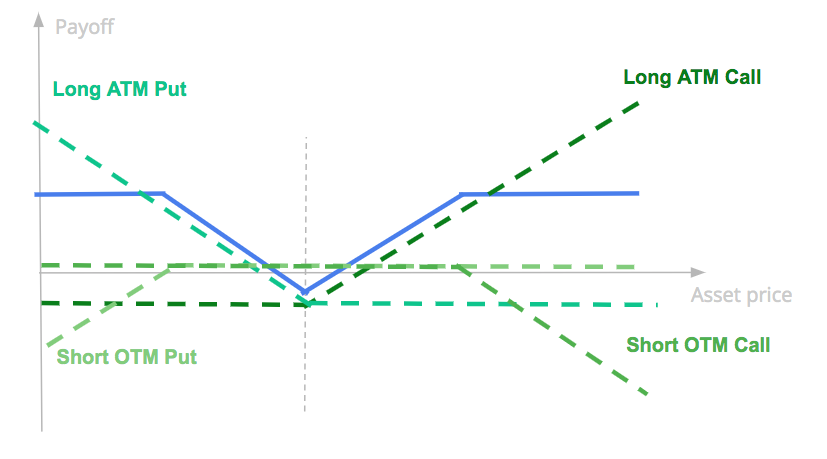
Such strategy is named short iron butterfly.

It has a negative premium if we buy and sell the same number of options, as the cost of the long straddle option is higher than the positive premium of the short strangle option, with strikes more OTM.

Such strategy makes sense for investors betting on asset movements with a certain range, on the upside or on the downside. If the underlying asset does not move, or has a very limited movement it is likely to have a negative P&L as the strategy has a negative premium. If the movement of the underlying asset is high enough, on the upside or on the downside the strategy is likely to post some gains at maturity. But if the underlying asset has an important movement on the upside or on the downside gains are capped.

40. What is the volga or vomma risk of an option?

The volga or vomma measures the sensitivity of the vega to a change in the implied volatility.  It is the second order partial derivative of the price of the option with respect to the implied volatility.

The volga risk is associated to the risk of important movements of the implied volatility, so to the volatility of volatility, or vol of vol risk. A higher vol of vol means more risk to have important price movements both on the downside or on the upside, so more tail risk on both sides.

41. Which of the two option strategies, straddle or strangle, has the higher volga exposure?

When looking at the sensitivity of the vega to changes in volatility, the vega of ATM options is not sensitive to volatility changes meaning a close to zero volga while OTM put or call options have a positive one, the vega increases with volatility. The volga risk, or vol of vol risk is attributed to the wings. 

The vega is higher for ATM options than OTM ones. However, an OTM option will be more similar to an ATM one when the implied volatility increases, as it becomes more likely to be exercised. So the vega of an OTM option increases with implied volatility, meaning a positive volga. 

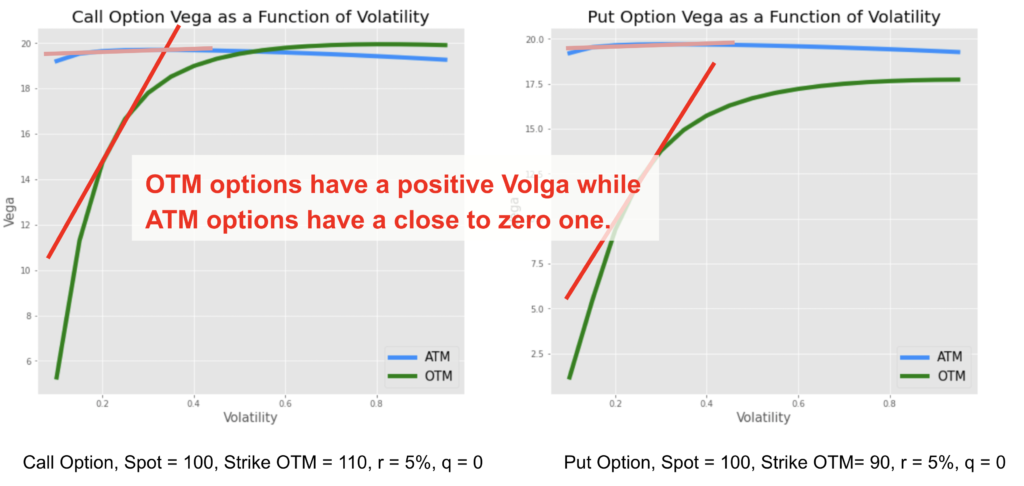
So a strangle option strategy, which is a combination of long OTM call and put options is likely to have a higher volga exposure compared to a straddle option strategy which is a combination of ATM call and put options.

42. So which strategy would you propose in order to have a positive volga exposure, and a close to zero exposure to other greeks?

A short iron butterfly strategy will be mostly exposed to the volga risk. The long strangle will have a positive volga exposure, while the short straddle strategy will have a close to zero volga exposure. All other major Greek exposures will be close to zero.

Both strategies will have a close to delta exposure.

The gamma and vega exposure of the long leg and the short leg will offset each other, particularly if we design the strategy to be gamma flat, selling more strangle options to offset the negative gamma of the short straddle.

The vanna exposure, sensitivity of the delta to a change of volatility will be low as well. ATM options have a low vanna exposure. It is not the case for OTM options, but an important part of the negative vanna of the short OTM call will be offset by the positive vanna of the OTM short put.

Below is a series of questions related to digital (or binary) options:

43. What is the payoff of a digital (or binary) cash-or-nothing call option? Can you draw it?

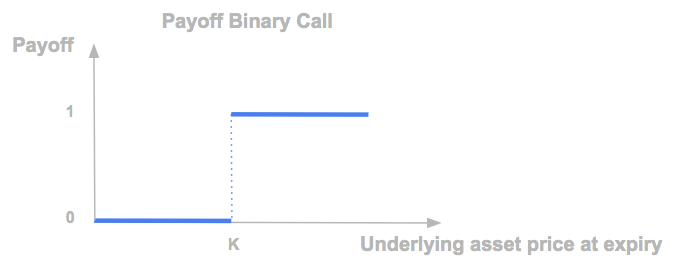
A binary (or digital) cash-or-nothing call option has the following payoff at the maturity of the option, with K the strike price and S the underlying asset. It is equal to 0 if the underlying asset price is below the strike price at maturity, and equal to 1 if it is above.

44. How can you replicate this payoff with two call options?

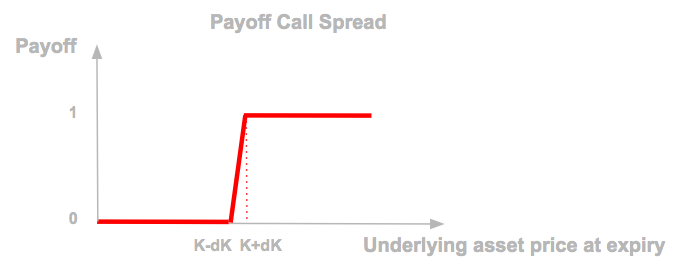
This payoff can be replicated by a call spread buying a call with strike K1 = K – dK and selling a call with strike K2 = K + dK in a quantity equal to 1 / (2 x dK) with dK small enough.

45. If we assume that the only changing variable is the strike price, can you express the price of the binary call as the derivatives of the price of a vanilla call option?

If we assume that the only changing variable is the strike price, the price of a binary call is equal to the opposite of the derivatives of the call price with respect to the strike price:

46. Can you approximate it by finite difference?

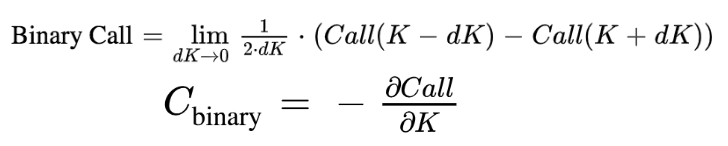
It can be approximated by finite difference as following, with ẟK a small change of K.

47. What is the price of the binary option in the Black-Scholes framework?

The price of the binary call is equal to the probability that the option will be exercised times the discount factor.

48. What if volatility is no more constant? We assume that the Black-Scholes implied volatility is no more constant, it is a function of the strike price. σ(K) is the implied volatility of a call option at the strike K. What is the price of the binary call option in this framework?

We have:

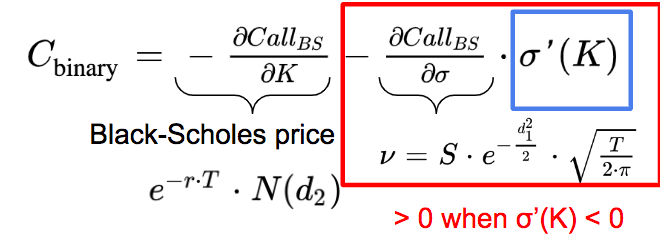
The price of a binary call is equal to the opposite of the derivatives of the call price with respect to the strike price.

So we obtain the following expression for the price of the binary call option:

49. If we assume that the implied volatility is a downward sloping function of the strike price, is the price of the binary call option higher or lower than the Black-Scholes price?

The first term is the Black-Scholes price, while the second term is the opposite of the product of the Black-Scholes vega and the derivatives of the volatility with respect to the strike price (the skew), which we assume is negative.

So the price of the binary call option is higher than the Black-Scholes price.

50. Is it still true for a binary put option?

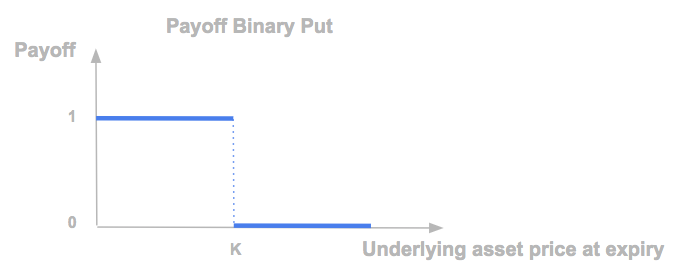
A binary put option can be replicated by a put spread.

If we assume that the only changing variable is the strike price, the price of a binary put is equal to the derivatives of the call price with respect to the strike price:

We assume that the Black-Scholes implied volatility is a decreasing function of the strike price we get:

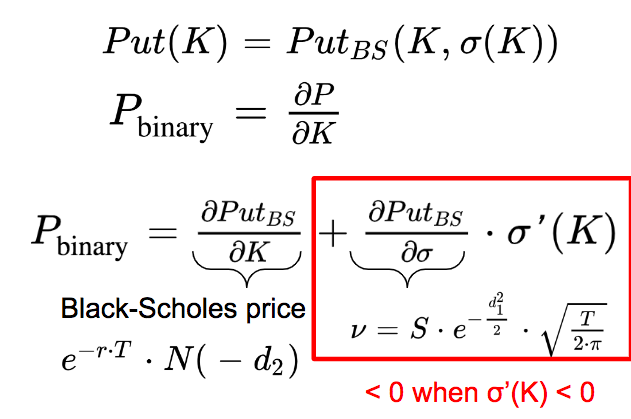
So we see that the price of the binary put option is lower than its Black-Scholes price.