Introduction to Stochastic Volatility Models

We will introduce in this post stochastic volatility models. They assume that the asset price but also its variance follow stochastic processes.

Such models are used in finance to simulate the price of the underlying asset and then to value options.

They are able to explain with a few additional parameters why the Black-Scholes implied volatilities with different strike prices or different time to maturities are different.

Black-Scholes Model and its Limits

In the famous black scholes model, the asset price is stochastic, it follows a geometric brownian motion,

The log return follows a gaussian distribution in this framework.

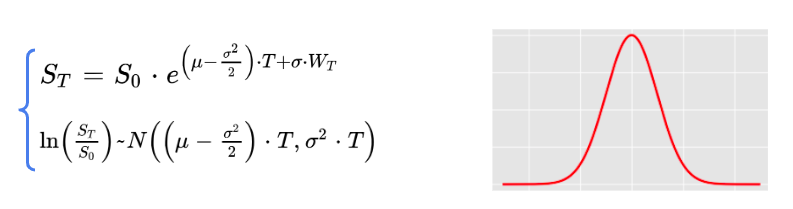
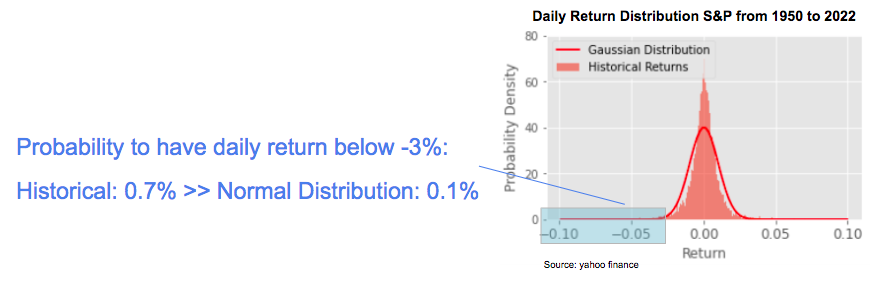
But this is not true in practice, historical returns are not normally distributed in general, they have fatter tails.

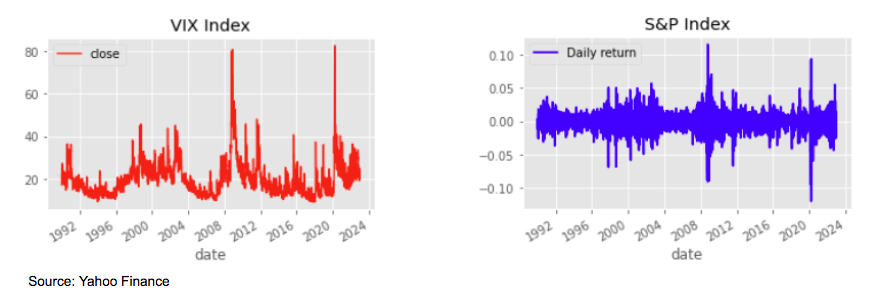
If we look for example at the daily returns of the S&P from 1950 to 2022, the historical probability to have a daily return below -3% would be close to 0.7%, while we would have estimated it at 0.1% with a gaussian distribution, so a factor 7 between the two.

In the Black-Scholes model, the volatility is assumed to be constant.

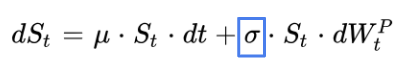
But this is not true in practice. Volatilities implied by option prices with different strikes or time-to-maturity are different.

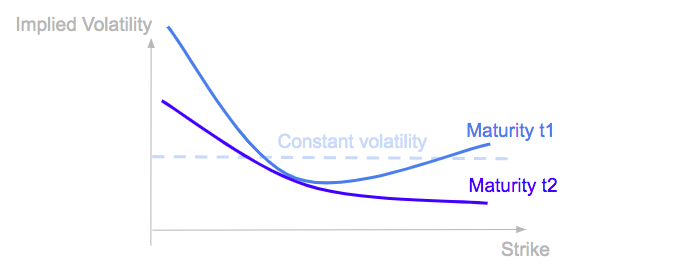
In practice the volatility changes with time and we tend to observe higher volatilities in periods of market stress when stock returns are more negative. 

Stochastic Volatility Models

All of this motivates to assume that not only the asset price (S) is stochastic but also its variance (ν).

We assume in the previous expression that the asset price S follows a process quite similar to the geometric brownian motion in the Black Scholes model, but now we assume as well that its variance ν follows a stochastic process as well.

μ is the drift of the asset price.

The choice of the two functions α and β will determine how the volatility behave. If we assume that both α and β are equal to zero, then the variance is no more stochastic, it is constant equal to the initial variance ν₀. We are back in the Black-Scholes framework. 

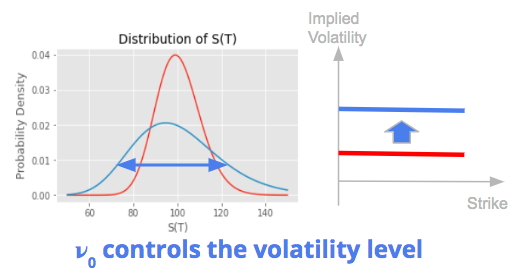
The initial variance ν₀ controls the volatility level.

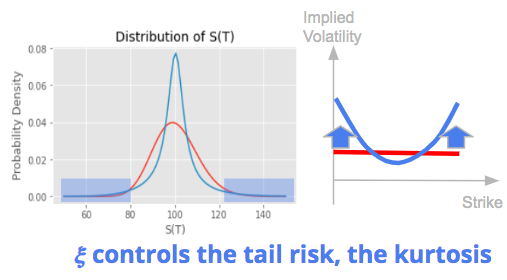
ξ is the volatility of volatility.  A higher volatility of volatility increases the probability to have extreme movements on both sides. It increases the tail risk of the return distribution. This translates into higher risk and higher prices for out-of-the-money options and an increase of the implied volatility on the wings creating a volatility smile.

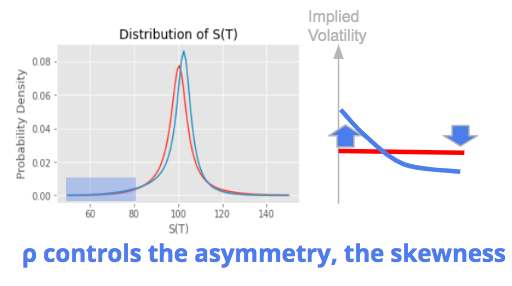
ρ is the correlation between the two brownian motion. It measures the correlation between the asset return and the change of the variance, it controls the spot / vol correlation. A negative correlation would mean that negative returns tend to come with higher volatility. This is typically what we observe on the stock market, with higher volatility in crisis periods. 

This parameter controls the asymmetry of the return distribution, its skewness. A negative spot / vol correlation will typically increase the probability to have very negative returns and reduce the probability to have very positive returns.

This translates into higher risk / higher price and so higher implied volatility for out-of-the-money put options on the left side, and lower risk / lower price and so lower implied volatility for out-of-the-money call options on the right side. The implied volatility is said to have a negative skew in this case, with an asymmetric curve and higher implied volatilities for low strike prices on the left compared to high strike prices on the right.

The Heston Model

The Heston model is one of the most famous stochastic volatility model.

It assumes that the variance follows a mean-reverting process, θ being the long term mean of the variance, and κ controlling the speed of reversion.

Heston is a special case of the general expression seen before with:

The Heston model has been quickly popular as it leads to an explicit analytic formula through an integral for the pricing of European call and put options.

Watch the videos introducing the Heston model.

The SABR Model

The SABR Model

SABR for Stochastic Alpha Beta Rho is another popular stochastic volatility model. The model was developed by Hagan et al. to model the dynamic of forward rates.

It has a different form compared to the general expression seen before, but it still has the three parameters controlling the second, third and fourth moments of the return distribution.

The volatility level is controlled by the initial variance α₀ in this case, the kurtosis via the volatility of volatility and the skewness via the correlation parameter. β tends to control as well the volatility skew and is often fixed at 0.5 in practice.

There is no closed form solution for the pricing of vanilla options under SABR model, except in the special cases where β = 0 or 1, but we get good asymptotic estimations and an expression of the Black-Scholes implied volatility as a function of SABR parameters.

It allows to fit relatively well the observed volatilities implied from option prices for a given maturity with few parameters and it can be useful to interpolate or extrapolate it.

Watch the video introducing the SABR model:

Watch the Video

Watch the Video

Save 10% on All Quant Next Courses with the Coupon Code: QuantNextBlog10

For students and graduates: We offer a 50% discount on all courses, please contact us if you are interested: contact@quant-next.com